An enzyme acts as a catalyst for a certain chemical reaction. This means that the enzyme decreases the activation energy and reaction time for the reaction without changing the equilibrium. The enzyme is neither consumed nor modified in the reaction. An enzyme-catalyzed reaction starts with the formation of an enzyme-substrate complex, ES.
The complex has two possible outcomes. It can dissociate to free enzyme (E) and substrate (S) with a rate constant k2 , or it can proceed to form product (P) with a rate constant k3 . At a fixed concentration of the enzyme the product is formed at a rate linearly proportional to the substrate concentration. However, after saturation of the active site of each enzyme molecule with its substrate the rate of product formation is independent of the substrate concentration, [S]. The equilibrium in (1) can be pushed towards product formation by increasing the substrate concentration.
![]() (1)
(1)
The rate of product formation depends on the concentration of enzyme-substrate complex.
![]() (2)
(2)
The rates of formation and consumption of ES can be written as:
rate of formation of ES
![]() (3)
(3)
rate of consumption of ES
![]() (4)
(4)
At steady state, [ES] is constant and the rates in (3) and (4) are equal:
![]() (5)
(5)
Rearrangement of (5) gives an expression for [ES] at steady state:
![]() (6)
(6)
The Michaelis constant, Km, is defined below:
![]() (7)
(7)
The concentration of free enzyme [E] equals the total enzyme concentration minus the concentration of enzyme-substrate complex:
![]() (8)
(8)
Substitution of (7) and (8) into (6) gives:
![]() (9)
(9)
Substituting this expression for [ES] in (2) gives:
![]() (10)
(10)
The reaction reaches its maximal rate, Vmax, when all active sites of the enzyme are occupied, i.e. when [S] is much larger than Km, which means that [S]/[S]+Km approaches 1.
Thus,
![]() (11)
(11)
these conditions product molecules are formed at a constant and maximal velocity. Equation (11) can also be written as:
![]() (12)
(12)
k3 reflects the turnover number, which is the maximal number of substrate molecules that can be converted to product per time unit, dimension time -1.
The Michaelis-Menten equation (13) is obtained from (10) and (11) and explains the relationship between reaction rate and substrate concentration as shown in Figure 5.
![]()
(13)
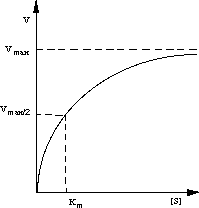 Figure 5. Reaction rate V versus substrate concentration [S] for an enzyme-catalyzed reaction.
Figure 5. Reaction rate V versus substrate concentration [S] for an enzyme-catalyzed reaction.
At a low substrate concentration ([S] << Km), then
![]() (14)
(14)
i.e. the rate is directly proportional to [S].
This means that an increase in substrate concentration will cause an increase in the reaction rate. On the other hand, at a high substrate concentration ([S] >> Km), then
![]() (15)
(15)
i.e. the reaction rate is independent of [S].
A special situation can be identified when the substrate concentration equals Km ([S] = Km); then
![]() (16)
(16)
which means that the Michaelis constant Km is equal to the substrate concentration at which the reaction rate is exactly half the maximum rate or Vmax/2.
The Michaelis-Menten equation (13) is transformed into an equation giving a straight line plot by taking the reciprocal of both sides of the equation.
![]() (17)
(17)
A plot of 1/V versus 1/[S] is called the Lineweaver-Burk plot or double-reciprocal plot, and has the intercept 1/Vmax and the slope Km/Vmax. Thus, the kinetic parameters Km and Vmax are readily derived by measuring the rate of catalysis at different substrate concentrations.
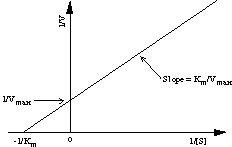 Figure 6. The Lineweaver-Burk plot
Figure 6. The Lineweaver-Burk plot
Multiplication of both sides of equation (17) with the substrate concentration [S] gives
![]() (18)
(18)
The plot of [S]/V versus [S] is sometimes referred to as the Hanes plot. The advantage of the Hanes plot over the Lineweaver-Burk plot is that the experimental errors in V give in the former a more or less constant contribution over a wide range of [S] values (15). Consequently, more accurate results are obtained using the Hanes procedure for data treatment.
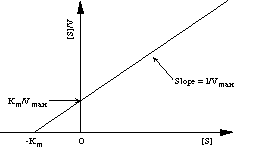 Figure 7. The Hanes plot
Figure 7. The Hanes plot
